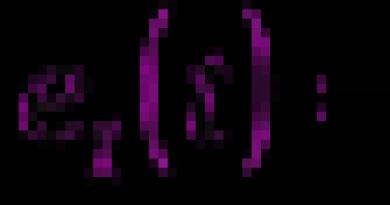فاصله از نقطه به نقطه، فرمول ها، مثال ها، راه حل ها. فاصله بین دو نقطه فاصله بین نقاط در فرمول صفحه مختصات

اجازه دهید یک سیستم مختصات مستطیلی داده شود.

قضیه 1.1.برای هر دو نقطه M 1 (x 1; y 1) و M 2 (x 2;y 2) صفحه، فاصله d بین آنها با فرمول بیان می شود.

اثباتاجازه دهید عمودهای M 1 B و M 2 A را به ترتیب از نقاط M 1 و M 2 رها کنیم.

روی محور Oy و Ox و نقطه تقاطع خطوط M 1 B و M 2 A را با K نشان دهید (شکل 1.4). موارد زیر ممکن است:

1) نقاط M 1، M 2 و K متفاوت است. بدیهی است که نقطه K مختصاتی دارد (x 2;y 1). به راحتی می توان فهمید که M 1 K = ôx 2 – x 1 ô، M 2 K = ôу 2 – y 1 ô. زیرا ∆M 1 KM 2 مستطیل شکل است، سپس با قضیه فیثاغورث d = M 1 M 2 = = .

2) نقطه K با نقطه M 2 منطبق است، اما با نقطه M 1 متفاوت است (شکل 1.5). در این مورد y 2 = y 1

و d = M 1 M 2 = M 1 K = ôx 2 – x 1 ô= =

3) نقطه K با نقطه M 1 منطبق است، اما با نقطه M 2 متفاوت است. در این مورد x 2 = x 1 و d =

M 1 M 2 = KM 2 = ôу 2 - y 1 ô= = .

4) نقطه M 2 با نقطه M 1 منطبق است. سپس x 1 = x 2، y 1 = y 2 و

d = M 1 M 2 = O = .

تقسیم بندی از این نظر.

اجازه دهید یک قطعه دلخواه M 1 M 2 در صفحه داده شود و اجازه دهید M ─ هر نقطه از این

بخش متفاوت از نقطه M 2 (شکل 1.6). عدد l که با برابری l = تعریف می شود ، تماس گرفت نگرش،در آن نقطه M قطعه M 1 M 2 را تقسیم می کند.

قضیه 1.2.اگر نقطه M(x;y) قطعه M 1 M 2 را نسبت به l تقسیم کند، مختصات این نقطه با فرمول تعیین می شود.

x = ، y = , (4)

که در آن (x 1;y 1) ─ مختصات نقطه M 1، (x 2;y 2) ─ مختصات نقطه M 2.

اثباتاجازه دهید اولین فرمول (4) را اثبات کنیم. فرمول دوم به روشی مشابه اثبات شده است. دو مورد احتمالی وجود دارد.

x = x 1 = = = .

2) خط مستقیم M 1 M 2 بر محور Ox عمود نیست (شکل 1.6). اجازه دهید عمودها را از نقاط M 1، M، M 2 به محور Ox پایین بیاوریم و نقاط تقاطع آنها را با محور Ox به ترتیب P 1، P، P 2 تعیین کنیم. با قضیه قطعات متناسب = l.

زیرا P 1 P = ôx – x 1 ô، PP 2 = ôx 2 – xô و اعداد (x – x 1) و (x 2 – x) علامت یکسانی دارند (در x 1< х 2 они положительны, а при х 1 >x 2 منفی هستند)، سپس

l = = ,

x - x 1 = l (x 2 - x)، x + lx = x 1 + lx 2،

x = .

نتیجه 1.2.1.اگر M 1 (x 1; y 1) و M 2 (x 2; y 2) دو نقطه دلخواه باشند و نقطه M(x;y) وسط پاره M 1 M 2 باشد،

x = ، y = (5)

اثباتاز آنجایی که M 1 M = M 2 M، پس l = 1 و با استفاده از فرمول (4) فرمول (5) را به دست می آوریم.

مساحت یک مثلث.

قضیه 1.3.برای هر نقطه A (x 1; y 1)، B (x 2; y 2) و C (x 3; y 3) که روی هم قرار ندارند

خط مستقیم، مساحت S مثلث ABC با فرمول بیان می شود

S = ô(x 2 – x 1)(y 3 – y 1) – (x 3 – x 1)(y 2 – y 1)ô (6)

اثباتناحیه ∆ ABC نشان داده شده در شکل. 1.7 به صورت زیر محاسبه می کنیم

S ABC = S ADEC + S BCEF – S ABFD .

ما مساحت ذوزنقه ها را محاسبه می کنیم:

S ADEC =
,

S BCEF =

S ABFD =

حالا داریم

S ABC = ((x 3 - x 1) (y 3 + y 1) + (x 3 - x 2) (y 3 + y 2) - (x 2 - -x 1) (y 1 + y 2)) = (x 3 y 3 – x 1 y 3 + x 3 y 1 – x 1 y 1 + + x 2 y 3 – -x 3 y 3 + x 2 y 2 – x 3 y 2 – x 2 y 1 + x 1 y 1 – x 2 y 2 + x 1 y 2) = (x 3 y 1 – x 3 y 2 + x 1 y 2 – x 2 y 1 + x 2 y 3 –

X 1 y 3) = (x 3 (y 1 – y 2) + x 1 y 2 – x 1 y 1 + x 1 y 1 – x 2 y 1 + y 3 (x 2 – x 1)) = (x 1 (y 2 – y 1) – x 3 (y 2 – y 1) + +y 1 (x 1 – x 2) – y 3 (x 1 – x 2)) = ((x 1 – x 3)( y 2 – y 1) + (x 1 – x 2)(y 1 – y 3)) = ((x 2 – x 1)(y 3 – y 1) –

- (x 3 - x 1) (y 2 - y 1)).

برای مکان دیگری ∆ ABC، فرمول (6) به روشی مشابه ثابت شده است، اما ممکن است با علامت "-" معلوم شود. بنابراین در فرمول (6) علامت مدول را قرار دادند.

سخنرانی 2.

معادله یک خط مستقیم در یک صفحه: معادله یک خط مستقیم با یک ضریب اصلی، معادله کلی یک خط مستقیم، معادله یک خط مستقیم در پاره‌ها، معادله یک خط مستقیم که از دو نقطه عبور می‌کند. زاویه بین خطوط مستقیم، شرایط موازی بودن و عمود بودن خطوط مستقیم در یک صفحه.

2.1. اجازه دهید یک سیستم مختصات مستطیلی و مقداری خط L روی صفحه داده شود.

تعریف 2.1.معادله ای به شکل F(x;y) = 0 که متغیرهای x و y را به هم متصل می کند، نامیده می شود. معادله خط L(در یک سیستم مختصات معین)، اگر این معادله با مختصات هر نقطه ای که روی خط L قرار دارد برآورده شود، نه با مختصات هر نقطه ای که روی این خط قرار ندارد.

نمونه هایی از معادلات خطوط در یک صفحه.

1) خط مستقیمی را موازی با محور Oy سیستم مختصات مستطیلی در نظر بگیرید (شکل 2.1). اجازه دهید نقطه تلاقی این خط را با محور Ox با حرف A نشان دهیم، (a;o) ─ آن یا-

دینات معادله x = a معادله خط داده شده است. در واقع، این معادله با مختصات هر نقطه M(a;y) این خط ارضا می شود و با مختصات هیچ نقطه ای که روی خط قرار ندارد ارضا نمی شود. اگر a = 0 باشد، خط مستقیم با محور Oy منطبق است که معادله x = 0 است.

2) معادله x - y = 0 مجموعه ای از نقاط صفحه را که نیمسازهای زوایای مختصات I و III را تشکیل می دهند، تعریف می کند.

3) معادله x 2 - y 2 = 0 ─ معادله دو نیمساز زوایای مختصات است.

4) معادله x 2 + y 2 = 0 یک نقطه O(0;0) را در صفحه تعریف می کند.

5) معادله x 2 + y 2 = 25 ─ معادله دایره ای به شعاع 5 با مرکز در مبدا.

فاصله بین دو نقطه در یک هواپیما.
دستگاه های مختصات

هر نقطه A از صفحه با مختصات آن (x, y) مشخص می شود. آنها با مختصات بردار 0A که از نقطه 0 خارج می شود - منشاء مختصات منطبق هستند.

فرض کنید A و B نقاط دلخواه صفحه با مختصات (x 1 y 1) و (x 2, y 2) باشند.

سپس بردار AB آشکارا دارای مختصاتی است (x 2 - x 1، y 2 - y 1). مشخص است که مجذور طول یک بردار برابر است با مجموع مجذور مختصات آن. بنابراین، فاصله d بین نقاط A و B، یا همان چیزی است که طول بردار AB است، از شرط تعیین می شود.

d 2 = (x 2 - x 1) 2 + (y 2 - y 1) 2.

d = \/ (x 2 - x 1) 2 + (y 2 - y 1) 2

فرمول به دست آمده به شما امکان می دهد فاصله بین هر دو نقطه در هواپیما را پیدا کنید، اگر فقط مختصات این نقاط مشخص باشد.

هر بار که در مورد مختصات یک نقطه خاص در صفحه صحبت می کنیم، منظور ما یک سیستم مختصات کاملاً تعریف شده x0y است. به طور کلی، سیستم مختصات در یک هواپیما را می توان به روش های مختلفی انتخاب کرد. بنابراین، به جای سیستم مختصات x0y، می توانید سیستم مختصات x"0y" را در نظر بگیرید که با چرخاندن محورهای مختصات قدیمی حول نقطه شروع 0 به دست می آید. پادساعتگردفلش ها در گوشه α .

اگر نقطه مشخصی از صفحه در سیستم مختصات x0y دارای مختصات (x,y) باشد، در سیستم مختصات جدید x"0y" مختصات متفاوتی خواهد داشت (x,y").

به عنوان مثال، نقطه M را در نظر بگیرید که روی محور 0x قرار دارد و از نقطه 0 در فاصله 1 جدا شده است.

بدیهی است که در سیستم مختصات x0y این نقطه دارای مختصاتی است (cos α ، گناه α ) و در سیستم مختصات x"0y" مختصات (1,0) است.

مختصات هر دو نقطه در صفحه A و B به نحوه تعیین سیستم مختصات در این صفحه بستگی دارد. اما فاصله این نقاط به روش تعیین سیستم مختصات بستگی ندارد. در پاراگراف بعدی از این شرایط مهم استفاده قابل توجهی خواهیم کرد.

تمرینات

I. فواصل بین نقاط صفحه را با مختصات بیابید:

1) (3.5) و (3.4)؛ 3) (0.5) و (5، 0)؛ 5) (-3،4) و (9، -17)؛

2) (2، 1) و (- 5، 1); 4) (0، 7) و (3،3)؛ 6) (8، 21) و (1، -3).

II. محیط مثلثی را بیابید که اضلاع آن با معادلات بدست آمده است:

x + y - 1 = 0، 2x - y - 2 = 0 و y = 1.

III. در سیستم مختصات x0y، نقاط M و N به ترتیب دارای مختصات (1، 0) و (0،1) هستند. مختصات این نقاط را در سیستم مختصات جدید که با چرخش محورهای قدیمی حول نقطه شروع با زاویه 30 درجه در خلاف جهت عقربه های ساعت به دست می آید، بیابید.

IV. در سیستم مختصات x0y، نقاط M و N دارای مختصات (2، 0) و (\) هستند. / 3/2، - 1/2) به ترتیب. مختصات این نقاط را در سیستم مختصات جدید که با چرخش محورهای قدیمی حول نقطه شروع با زاویه 30 درجه در جهت عقربه های ساعت به دست می آید، بیابید.

در این مقاله راه هایی برای تعیین فاصله از نقطه به نقطه به صورت نظری و با استفاده از مثال وظایف خاص بررسی خواهیم کرد. برای شروع، چند تعاریف را معرفی می کنیم.

تعریف 1

فاصله بین نقاططول بخش اتصال آنها در مقیاس موجود است. برای داشتن یک واحد طول برای اندازه گیری لازم است یک مقیاس تنظیم کنید. بنابراین، اساساً مشکل یافتن فاصله بین نقاط با استفاده از مختصات آنها در یک خط مختصات، در یک صفحه مختصات یا فضای سه بعدی حل می شود.

داده های اولیه: خط مختصات O x و یک نقطه دلخواه A روی آن قرار دارد. هر نقطه از خط دارای یک عدد واقعی است: بگذارید عدد معینی برای نقطه A باشد. x A,همچنین مختصات نقطه A است.

به طور کلی می توان گفت که طول یک قطعه معین در مقایسه با قطعه ای که به عنوان واحد طول در یک مقیاس معین گرفته می شود، ارزیابی می شود.

اگر نقطه A با یک عدد واقعی مطابقت دارد، با کنار گذاشتن متوالی از نقطه O به نقطه در امتداد خط مستقیم O A قطعات - واحدهای طول، می توانیم طول قطعه O A را از تعداد کل قطعات واحد کنار گذاشته شده تعیین کنیم.

به عنوان مثال، نقطه A مربوط به عدد 3 است - برای رسیدن به آن از نقطه O، باید سه بخش واحد را کنار بگذارید. اگر نقطه A دارای مختصات - 4 باشد، بخش های واحد به روشی مشابه، اما در جهت منفی متفاوت قرار می گیرند. بنابراین، در حالت اول، فاصله O A برابر با 3 است. در حالت دوم O A = 4.

اگر نقطه A یک عدد گویا به عنوان مختصات داشته باشد، از مبدا (نقطه O) یک عدد صحیح از بخش های واحد و سپس قسمت ضروری آن را رسم می کنیم. اما از نظر هندسی همیشه نمی توان اندازه گیری کرد. برای مثال، رسم کسری 4 111 روی خط مختصات دشوار به نظر می رسد.

با استفاده از روش فوق، رسم یک عدد غیر منطقی روی یک خط مستقیم کاملاً غیرممکن است. مثلاً وقتی مختصات نقطه A 11 باشد. در این مورد، می توان به انتزاع روی آورد: اگر مختصات داده شده نقطه A بزرگتر از صفر باشد، O A = x A (عدد به عنوان فاصله در نظر گرفته می شود). اگر مختصات کمتر از صفر باشد، O A = - x A . به طور کلی، این عبارات برای هر عدد واقعی x A صادق است.

به طور خلاصه: فاصله از مبدا تا نقطه ای که مطابق با یک عدد واقعی در خط مختصات است برابر است با:

• 0 اگر نقطه با مبدا منطبق باشد.

• x A، اگر x A > 0;

• - x A اگر x A< 0 .

در این صورت بدیهی است که طول قطعه به خودی خود نمی تواند منفی باشد، بنابراین با استفاده از علامت مدول فاصله نقطه O تا نقطه A را با مختصات می نویسیم. xA: O A = x A

جمله زیر درست خواهد بود: فاصله یک نقطه تا نقطه دیگر برابر مدول اختلاف مختصات خواهد بود.آن ها برای نقاط A و B که روی یک خط مختصات برای هر مکان قرار دارند و مختصات مربوطه دارند xAو x B: A B = x B - x A.

داده های اولیه: نقاط A و B که روی صفحه ای در یک سیستم مختصات مستطیلی O x y با مختصات داده شده قرار دارند: A (x A, y A) و B (x B, y B).

اجازه دهید از طریق نقاط A و B عمود بر محورهای مختصات O x و O y رسم کنیم و در نتیجه نقاط طرح را بدست آوریم: A x، A y، B x، B y. بر اساس مکان نقاط A و B، گزینه های زیر ممکن است:

اگر نقاط A و B بر هم منطبق باشند، فاصله بین آنها صفر است.

اگر نقاط A و B بر روی یک خط مستقیم عمود بر محور Ox (محور آبسیسا) قرار بگیرند، آنگاه نقاط بر هم منطبق هستند و | A B | = | A y B y | . از آنجایی که فاصله بین نقاط برابر با مدول اختلاف مختصات آنها است، A y B y = y B - y A و بنابراین A B = A y B y = y B - y A.

اگر نقاط A و B بر روی یک خط مستقیم عمود بر محور O y (محور مختصات) قرار بگیرند - بر اساس قیاس با پاراگراف قبلی: A B = A x B x = x B - x A

اگر نقاط A و B بر روی یک خط مستقیم عمود بر یکی از محورهای مختصات قرار نگیرند، با استخراج فرمول محاسبه فاصله بین آنها را خواهیم یافت:

می بینیم که مثلث A B C از نظر ساخت مستطیل شکل است. در این مورد، A C = A x B x و B C = A y B y. با استفاده از قضیه فیثاغورث، تساوی را ایجاد می کنیم: A B 2 = A C 2 + B C 2 ⇔ A B 2 = A x B x 2 + A y B y 2 و سپس آن را تبدیل می کنیم: A B = A x B x 2 + A y B y 2 = x B - x A 2 + y B - y A 2 = (x B - x A) 2 + (y B - y A) 2

بیایید از نتیجه به دست آمده نتیجه بگیریم: فاصله از نقطه A تا نقطه B در صفحه با محاسبه با استفاده از فرمول با استفاده از مختصات این نقاط تعیین می شود.

A B = (x B - x A) 2 + (y B - y A) 2

فرمول به دست آمده همچنین اظهارات قبلی را برای موارد تصادف نقاط یا موقعیت هایی که نقاط روی خطوط مستقیم عمود بر محورها قرار دارند تأیید می کند. بنابراین، اگر نقاط A و B بر هم منطبق باشند، برابری زیر درست خواهد بود: A B = (x B - x A) 2 + (y B - y A) 2 = 0 2 + 0 2 = 0

برای موقعیتی که نقاط A و B روی یک خط مستقیم عمود بر محور x قرار دارند:

A B = (x B - x A) 2 + (y B - y A) 2 = 0 2 + (y B - y A) 2 = y B - y A

برای حالتی که نقاط A و B بر روی یک خط مستقیم عمود بر محور قرار می گیرند:

A B = (x B - x A) 2 + (y B - y A) 2 = (x B - x A) 2 + 0 2 = x B - x A

داده های اولیه: یک سیستم مختصات مستطیلی O x y z با نقاط دلخواه که روی آن قرار گرفته اند با مختصات داده شده A (x A, y A, z A) و B (x B, y B, z B). تعیین فاصله بین این نقاط ضروری است.

بیایید حالت کلی را در نظر بگیریم که نقاط A و B در صفحه موازی با یکی از صفحات مختصات قرار نگیرند. اجازه دهید صفحات عمود بر محورهای مختصات را از طریق نقاط A و B رسم کنیم و نقاط طرح مربوطه را بدست آوریم: A x , A y , A z , B x , B y , B z

فاصله بین نقاط A و B قطر متوازی الاضلاع است. با توجه به ساخت و ساز اندازه گیری های این متوازی الاضلاع: A x B x، A y B y و A z B z

از درس هندسه می دانیم که مربع قطر یک متوازی الاضلاع برابر است با مجموع مجذورات ابعاد آن. بر اساس این عبارت، برابری را بدست می آوریم: A B 2 = A x B x 2 + A y B y 2 + A z B z 2

با استفاده از نتیجه گیری های قبلی، موارد زیر را می نویسیم:

A x B x = x B - x A، A y B y = y B - y A، A z B z = z B - z A

بیایید عبارت را تبدیل کنیم:

A B 2 = A x B x 2 + A y B y 2 + A z B z 2 = x B - x A 2 + y B - y A 2 + z B - z A 2 = = (x B - x A) 2 + (y B - y A) 2 + z B - z A 2

نهایی فرمول تعیین فاصله بین نقاط در فضابه این صورت خواهد بود:

A B = x B - x A 2 + y B - y A 2 + (z B - z A) 2

فرمول به دست آمده برای موارد زیر نیز معتبر است:

نقاط منطبق هستند.

آنها روی یک محور مختصات یا یک خط مستقیم موازی با یکی از محورهای مختصات قرار دارند.

نمونه هایی از حل مسائل در یافتن فاصله بین نقاط

مثال 1

داده های اولیه: یک خط مختصات و نقاطی که روی آن قرار دارند با مختصات A (1 - 2) و B (11 + 2) داده شده است. باید فاصله نقطه مبدا O تا نقطه A و بین نقاط A و B را پیدا کرد.

راه حل

1. فاصله نقطه مرجع تا نقطه برابر مدول مختصات این نقطه است، به ترتیب O A = 1 - 2 = 2 - 1
2. ما فاصله بین نقاط A و B را به عنوان مدول اختلاف بین مختصات این نقاط تعریف می کنیم: A B = 11 + 2 - (1 - 2) = 10 + 2 2

پاسخ: O A = 2 - 1، A B = 10 + 2 2

مثال 2

داده های اولیه: یک سیستم مختصات مستطیلی و دو نقطه روی آن A (1، - 1) و B (λ + 1، 3) داده شده است. λ مقداری واقعی است. لازم است تمام مقادیر این عدد را پیدا کنید که در آن فاصله A B برابر با 5 باشد.

راه حل

برای یافتن فاصله بین نقاط A و B باید از فرمول A B = (x B - x A) 2 + y B - y A 2 استفاده کنید.

با جایگزینی مقادیر مختصات واقعی، به دست می آوریم: A B = (λ + 1 - 1) 2 + (3 - (- 1)) 2 = λ 2 + 16

ما همچنین از شرط موجود استفاده می کنیم که A B = 5 و سپس برابری درست خواهد بود:

λ 2 + 16 = 5 λ 2 + 16 = 25 λ = 3 ±

پاسخ: اگر λ = 3 ± B = 5.

مثال 3

داده های اولیه: یک فضای سه بعدی در سیستم مختصات مستطیلی O x y z و نقاط A (1، 2، 3) و B - 7، - 2، 4 در آن مشخص شده است.

راه حل

برای حل مسئله از فرمول A B = x B - x A 2 + y B - y A 2 + (z B - z A) 2 استفاده می کنیم.

با جایگزینی مقادیر واقعی، دریافت می کنیم: A B = (- 7 - 1) 2 + (- 2 - 2) 2 + (4 - 3) 2 = 81 = 9

پاسخ: | A B | = 9

در صورت مشاهده خطایی در متن، لطفاً آن را برجسته کرده و Ctrl+Enter را فشار دهید

در اینجا یک ماشین حساب وجود خواهد داشت

فاصله بین دو نقطه در یک خط

خط مختصاتی را در نظر بگیرید که روی آن 2 نقطه مشخص شده است: A A آو B B ب. برای پیدا کردن فاصله بین این نقاط، باید طول قطعه را پیدا کنید A B AB A B. این کار با استفاده از فرمول زیر انجام می شود:

فاصله بین دو نقطه در یک خط

A B = ∣ a − b ∣ AB=|a-b|A B =∣a−ب∣,

جایی که الف، ب الف، ب الف، ب- مختصات این نقاط روی یک خط مستقیم (خط مختصات).

با توجه به اینکه فرمول دارای مدول است، هنگام حل آن، مهم نیست که کدام مختصات را از آن کم کنیم (زیرا قدر مطلق این تفاوت گرفته شده است).

∣ a − b ∣ = ∣ b − a ∣ |a-b|=|b-a|∣a−b ∣ =∣ b −الف∣

بیایید برای درک بهتر راه حل چنین مشکلاتی به یک مثال نگاه کنیم.

مثال 1

نقاط روی خط مختصات مشخص شده اند A A آ، که مختصات آن برابر است با 9 9 9 و دوره B B ببا مختصات − 1 -1 − 1 . ما باید فاصله بین این دو نقطه را پیدا کنیم.

راه حل

اینجا a = 9، b = − 1 a=9، b=-1 a =9، b =− 1

ما از فرمول استفاده می کنیم و مقادیر را جایگزین می کنیم:

A B = ∣ a − b ∣ = ∣ 9 − (− 1) ∣ = ∣ 10 ∣ = 10 AB=|a-b|=|9-(-1)|=|10|=10A B =∣a−b ∣ =∣ 9 − (− 1 ) ∣ = ∣ 1 0 ∣ = 1 0

پاسخ

فاصله بین دو نقطه در یک هواپیما

دو نقطه داده شده در یک هواپیما را در نظر بگیرید. از هر نقطه ای که روی هواپیما مشخص شده است، باید دو عمود را پایین بیاورید: به محور O X OX O Xو روی محور OY OY OY. سپس مثلث در نظر گرفته می شود A B C ABC A B C. از آنجایی که مستطیل شکل است ( B C قبل از میلاد قبل از میلاد مسیحعمود بر A C AC A C، سپس بخش را پیدا کنید A B AB A Bکه فاصله بین نقاط را نیز می توان با استفاده از قضیه فیثاغورث انجام داد. ما داریم:

A B 2 = A C 2 + B C 2 AB^2=AC^2+BC^2آ ب 2 = آ سی 2 + ب سی 2

اما، بر اساس این واقعیت است که طول A C AC A Cمساوی با x B - x A x_B-x_A ایکس ب​ − ایکس آ​ ، و طول B C قبل از میلاد قبل از میلاد مسیحمساوی با y B − y A y_B-y_A y ب​ − y آ​ ، این فرمول را می توان به صورت زیر بازنویسی کرد:

فاصله بین دو نقطه در یک هواپیما

A B = (x B - x A) 2 + (y B - y A) 2 AB=\sqrt((x_B-x_A)^2+(y_B-y_A)^2)A B =(ایکس ب​ − ایکس آ​ ) 2 + (y ب​ − y آ​ ) 2 ​ ,

جایی که x A، y A x_A، y_A ایکس آ​ , y آ​ و x B، y B x_B، y_B ایکس ب​ , y ب​ - مختصات نقاط A A آو B B ببه ترتیب.

مثال 2

لازم است فاصله بین نقاط را پیدا کنید سی سی سیو اف اف اف، اگر مختصات اول باشد (8 ; − 1) (8;-1) (8 ; − 1 ) و دوم - (4 ; 2) (4;2) (4 ; 2 ) .

راه حل

X C = 8 x_C = 8 ایکس سی​ = 8
y C = - 1 y_C=-1 y سی​ = − 1
x F = 4 x_F = 4 ایکس اف​ = 4
y F = 2 y_F = 2 y اف​ = 2

C F = (x F - x C) 2 + (y F - y C) 2 = (4 - 8) 2 + (2 - (-1)) 2 = 16 + 9 = 25 = 5 CF=\sqrt(( x_F-x_C)^2+(y_F-y_C)^2)=\sqrt((4-8)^2+(2-(-1))^2)=\sqrt(16+9)=\sqrt( 25) = 5C F =(ایکس اف​ − ایکس سی​ ) 2 + (y اف​ − y سی​ ) 2 ​ = (4 − 8 ) 2 + (2 − (− 1 ) ) 2 ​ = 1 6 + 9 ​ = 2 5 ​ = 5

پاسخ

فاصله بین دو نقطه در فضا

یافتن فاصله بین دو نقطه در این حالت مشابه مورد قبلی است، با این تفاوت که مختصات نقطه در فضا با سه عدد مشخص می شود؛ بر این اساس، مختصات محور مورد نظر نیز باید به فرمول اضافه شود. فرمول به صورت زیر خواهد بود:

فاصله بین دو نقطه در فضا

A B = (x B - x A) 2 + (y B - y A) 2 + (z B - z A) 2 AB=\sqrt((x_B-x_A)^2+(y_B-y_A)^2+( z_B-z_A)^2)A B =(ایکس ب​ − ایکس آ​ ) 2 + (y ب​ − y آ​ ) 2 + (z ب​ − zآ​ ) 2 ​

مثال 3

طول قطعه را پیدا کنید FK FKافکدر فضا اگر مختصات نقاط انتهای آن به صورت زیر باشد: (− 1 ; − 1 ; 8) (-1;-1;8) (− 1 ; − 1 ; 8 ) و (− 3 ; 6 ; 0) (-3;6;0) (− 3 ; 6 ; 0 ) . جواب را به نزدیکترین عدد صحیح گرد کنید.

راه حل

$اف=(-1;-1;8)K\; =\; (-\; 3\; ;\; 6\; ;\; 0)\; K=(-3;6;0)ک=(-3;6;0)$

$افک=\sqrt{({ایکس}^{ک-{ایکس}^{اف{)}^{2+(y^{ک-y^{اف{)}^{2+(z^{ک-z^{اف{)}^{2=\sqrt{(-3-(-1){)}^{2+(6-(-1){)}^{2+(0-8{)}^{2=\sqrt{117\approx 10.8}}}}}}}}}}}}}}}$

با توجه به شرایط مسئله، باید پاسخ را به یک عدد کامل گرد کنیم.

محاسبه فواصل بین نقاط بر اساس مختصات آنها در یک صفحه ابتدایی است؛ در سطح زمین کمی پیچیده تر است: ما اندازه گیری فاصله و آزیموت اولیه بین نقاط را بدون تبدیل طرح ریزی در نظر خواهیم گرفت. ابتدا بیایید اصطلاحات را درک کنیم.

معرفی

طول قوس دایره بزرگ- کوتاهترین فاصله بین هر دو نقطه واقع در سطح یک کره که در امتداد خطی که این دو نقطه را به هم متصل می کند اندازه گیری می شود (به چنین خطی ارتودرومی می گویند) و از امتداد سطح کره یا سطح دیگر چرخش عبور می کند. هندسه کروی با هندسه معمولی اقلیدسی متفاوت است و معادلات فاصله نیز شکل متفاوتی به خود می گیرند. در هندسه اقلیدسی کوتاهترین فاصله بین دو نقطه یک خط مستقیم است. روی یک کره، هیچ خط مستقیمی وجود ندارد. این خطوط روی کره بخشی از دایره های بزرگ هستند - دایره هایی که مرکز آنها با مرکز کره منطبق است. آزیموت اولیه- آزیموت، با گرفتن آن هنگام شروع حرکت از نقطه A، دنبال کردن دایره بزرگ برای کوتاهترین فاصله تا نقطه B، نقطه پایانی نقطه B خواهد بود. هنگامی که از نقطه A به نقطه B در امتداد خط دایره بزرگ حرکت می کنیم، آزیموت از موقعیت فعلی به نقطه پایانی B ثابت است در حال تغییر است. آزیموت اولیه با یک ثابت متفاوت است که به دنبال آن آزیموت از نقطه فعلی تا نقطه نهایی تغییر نمی کند، اما مسیر طی شده کوتاه ترین فاصله بین دو نقطه نیست.

از طریق هر دو نقطه روی سطح یک کره، اگر مستقیماً مخالف یکدیگر نباشند (یعنی پادپای نباشند)، می توان یک دایره بزرگ منحصر به فرد رسم کرد. دو نقطه یک دایره بزرگ را به دو قوس تقسیم می کنند. طول یک قوس کوتاه کوتاه ترین فاصله بین دو نقطه است. بی نهایت دایره بزرگ را می توان بین دو نقطه پادپای رسم کرد، اما فاصله بین آنها در هر دایره یکسان و برابر با نصف محیط دایره خواهد بود، یا π*R که در آن R شعاع کره است.

در یک صفحه (در یک سیستم مختصات مستطیلی)، دایره‌های بزرگ و تکه‌های آن‌ها، همانطور که در بالا ذکر شد، نشان‌دهنده کمان‌ها در همه برجستگی‌ها هستند، به‌جز گنومونیک، که در آن دایره‌های بزرگ خطوط مستقیم هستند. در عمل، این بدان معنی است که هواپیماها و سایر حمل و نقل هوایی همیشه از مسیر حداقل فاصله بین نقاط برای صرفه جویی در سوخت استفاده می کنند، یعنی پرواز در امتداد یک فاصله دایره ای بزرگ انجام می شود، در هواپیما مانند یک قوس به نظر می رسد.

شکل زمین را می توان به عنوان یک کره توصیف کرد، بنابراین معادلات فاصله دایره بزرگ برای محاسبه کوتاه ترین فاصله بین نقاط روی سطح زمین مهم هستند و اغلب در ناوبری استفاده می شوند. محاسبه فاصله با این روش کارآمدتر و در بسیاری موارد دقیق‌تر از محاسبه آن برای مختصات پیش‌بینی‌شده (در سیستم‌های مختصات مستطیلی) است، زیرا اولاً نیازی به تبدیل مختصات جغرافیایی به یک سیستم مختصات مستطیلی (انجام تبدیل‌های طرح‌ریزی) نیست. ثانیاً، بسیاری از برجستگی‌ها، در صورت انتخاب نادرست، می‌توانند به دلیل ماهیت اعوجاج‌های برآمدگی منجر به اعوجاج طول قابل توجهی شوند. مشخص است که این یک کره نیست، بلکه یک بیضی است که شکل زمین را با دقت بیشتری توصیف می کند، با این حال، این مقاله محاسبه فواصل را به طور خاص روی یک کره مورد بحث قرار می دهد؛ برای محاسبات، از کره ای با شعاع 6372795 متر استفاده می شود. ، که می تواند منجر به خطا در محاسبه فواصل در حد 0.5٪ شود.

فرمول ها

سه راه برای محاسبه فاصله کروی دایره بزرگ وجود دارد. 1. قضیه کسینوس کرویدر مورد فواصل کوچک و عمق محاسباتی کوچک (تعداد ارقام اعشاری)، استفاده از فرمول می تواند منجر به خطاهای گرد کردن قابل توجهی شود. φ1, λ1; φ2, λ2 - طول و عرض جغرافیایی دو نقطه بر حسب رادیان Δλ - تفاوت مختصات در طول جغرافیایی Δδ - اختلاف زاویه ای Δδ = arccos (sin φ1 sin φ2 + cos φ1 cos φ2 cos Δλ) برای تبدیل فاصله زاویه ای به متریک باید اختلاف زاویه را در شعاع زمین ضرب کنید (6372795 متر)، واحدهای فاصله نهایی برابر با واحدهایی که شعاع در آنها بیان می شود (در این مورد متر) خواهد بود. 2. فرمول هاورسینبرای جلوگیری از مشکلات در مسافت های کوتاه استفاده می شود. 3. اصلاح برای آنتی پادهافرمول قبلی نیز مشمول مشکل نقاط پادپای است که برای حل آن از اصلاح زیر استفاده می شود.

پیاده سازی من در PHP

// شعاع زمین define("EARTH_RADIUS", 6372795); /* * فاصله بین دو نقطه * $φA، $λA - عرض جغرافیایی، طول جغرافیایی نقطه 1، * $φB، $λB - عرض جغرافیایی، طول جغرافیایی نقطه دوم * نوشته شده بر اساس http://gis-lab.info/ qa/great-circles.html * میخائیل کوبزارف< >* */ تابع محاسبهTheDistance ($φA, $λA, $φB, $λB) ( // تبدیل مختصات به رادیان $lat1 = $φA * M_PI / 180؛ $lat2 = $φB * M_PI / 180؛ $long1 = $λA * M_PI / 180؛ $long2 = $λB * M_PI / 180؛ // کسینوس و سینوس تفاوت‌های طول و عرض جغرافیایی $cl1 = cos($lat1)؛ $cl2 = cos($lat2)؛ $sl1 = sin($lat1) ) ؛ $sl2 = sin($lat2)؛ $delta = $long2 - $long1؛ $cdelta = cos($delta)؛ $sdelta = sin($delta)؛ // محاسبات طول دایره بزرگ $y = sqrt(pow ( $cl2 * $sdelta, 2) + pow($cl1 * $sl2 - $sl1 * $cl2 * $cdelta, 2))؛ $x = $sl1 * $sl2 + $cl1 * $cl2 * $cdelta؛ / / $ad = atan2($y، $x)؛ $dist = $ad * EARTH_RADIUS؛ return $dist؛ ) مثالی از فراخوانی تابع: $lat1 = 77.1539; $long1 = -139.398; $lat2 = -77.1804; $long2 = -139.55; echo accountTheDistance($lat1، $long1، $lat2، $long2). "متر"؛ // بازگشت "17166029 متر"

مقاله برگرفته از سایت